---
title: Are munis over-hedged with swaps? pt1 | Intuitive Analytics
description: Are munis over-hedged with swaps? pt1
image: https://www.intuitive-analytics.com/hs-fs/file-15737705-png/images/are_munis_over-hedged_with_swaps.png
---

# Are munis over-hedged with swaps? pt1

 Posted by Peter Orr on Jun 25, 2009

"Opportunity is missed by most people because it is dressed in overalls and looks like work."

- Thomas Edison

Over the last decade, many tax-exempt issuers have executed interest rate swaps based upon a percentage of the 1M or 3M London Interbank Bank Offered Rate in order to hedge the interest rate risk inherent in tax-exempt variable rate, or (perhaps unfortunately) auction rate securities. Whether or not these "synthetic fixed-rate" structures are appropriate for all or any tax-exempt issuers is a hot topic these days in light of expected regulatory changes, and one I'm not touching here. What I am going to discuss is something more fundamental to implementation: how does one arrive at the *best* structure to minimize overall debt service volatility, have historical practices led to chronic over-hedging and if so, what are the ramifications.

![Are munis over-hedged with swaps?](https://www.intuitive-analytics.com/hs-fs/file-15737705-png/images/are_munis_over-hedged_with_swaps.png?width=531&height=387&name=are_munis_over-hedged_with_swaps.png)

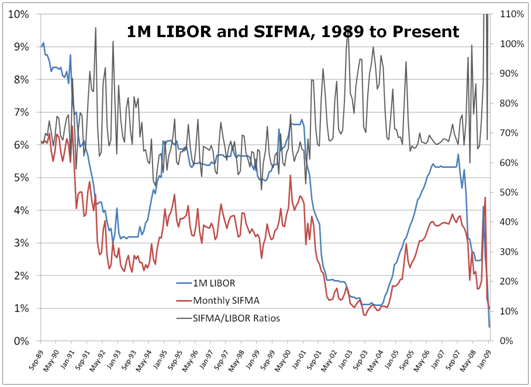
The usual methodology employed to determine the "right" percentage of LIBOR for the floating leg of the swap is usually calculated based upon some historic average of the ratio of the [SIFMA swap index](http://archives1.sifma.org/swapdata.html), a weekly tax-exempt floating index, to 1month or 3 month LIBOR. Ignoring tax and accounting issues for the moment, if the goal is to minimize the expected variability of overall net debt service payments this simple averaging method is incorrect in all cases save one: the expected correlation between SIFMA and LIBOR is precisely 1. My personal assessment is that most issuer/advisor/banker participants in this particular market are not accustomed to thinking explicitly about correlation as it relates to their risk management decisions. However, they're making implicit assessments of correlation quite often, sometimes with regrettable consequences.

Let me explain. Any recently test-taking CFA candidate (congratulations by the way) will tell you that the variance minimizing hedge ratio is calculated using the following simple formula:

Volhedged item / Volhedging item * Correlationbetween the 2

This formula has intuitive appeal. If the volatility of my hedging item is far greater than the item hedged, my hedge ratio should fall, which you can see it does. As it relates to correlation and in the canonical edge case, if I have a 0 expected correlation between the item I'm hedging and the item I'm hedging with, we'd expect our hedge ratio to be zero as well; you can't hedge something with something else if you expect no co-movement between the two items.

But is it our best judgment that (changes in) SIFMA and LIBOR will be perfectly correlated going forward? What does history tell us? If we look at the levels themselves, it's clear their correlation isn't perfect. Below are 5 year rolling correlations of one month averaged SIFMA and 1M LIBOR.

![Are munis over-hedged with swaps?](https://www.intuitive-analytics.com/hs-fs/file-15737753-png/images/are_munis_over-hedged_with_swaps_2.png?width=508&height=370&name=are_munis_over-hedged_with_swaps_2.png)

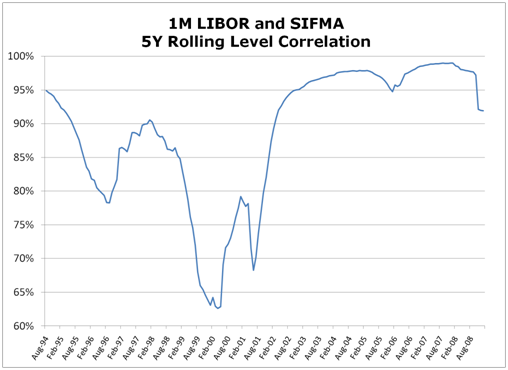
What does all this mean? If we expect that SIFMA LIBOR ratios will be 68% going forward (a common and frequently used historically calculated average ratio), then the right hedge ratio would scale this by our expected correlation which likely does not equal 1. A reasonable expected correlation between 85-90% would yield an optimal hedge ratio of between 57.8 and 61.2%. Some banks have gotten to numbers like this by performing regression calculations, which of course are just alternative ways of determining correlation.

So what and who cares? Well, let's compare an issuer with a 70% LIBOR swap paying a 3.5% fixed rate versus one with a 60% LIBOR swap with a 3% fixed rate. The latter has used roughly 14% less swap to do its hedging, which means the 60% LIBOR swap's value is less sensitive to changes in interest rates. This will have important ramifications for mark to markets and collateral posting. For more detail on that and how to capture these effects within a market model, stay tuned for [Part2](https://www.intuitive-analytics.com/blog/bid/13639/Are-munis-over-hedged-with-swaps-pt2).

### Comments

### Subscribe to our Articles

### Browse by Tag **

- [public finance (17)](https://www.intuitive-analytics.com/blog/topic/public-finance)
- [refunding (15)](https://www.intuitive-analytics.com/blog/topic/refunding)
- [public finance analytics (14)](https://www.intuitive-analytics.com/blog/topic/public-finance-analytics)
- [Financial Decisions (13)](https://www.intuitive-analytics.com/blog/topic/financial-decisions)
- [advance refunding (13)](https://www.intuitive-analytics.com/blog/topic/advance-refunding)
- [bond option (13)](https://www.intuitive-analytics.com/blog/topic/bond-option)
- [public finance software (12)](https://www.intuitive-analytics.com/blog/topic/public-finance-software)
- [call option (11)](https://www.intuitive-analytics.com/blog/topic/call-option)
- [interest rate model (9)](https://www.intuitive-analytics.com/blog/topic/interest-rate-model)
- [municipal finance software (9)](https://www.intuitive-analytics.com/blog/topic/municipal-finance-software)
- [SIFMA (8)](https://www.intuitive-analytics.com/blog/topic/sifma)
- [Financial Models (7)](https://www.intuitive-analytics.com/blog/topic/financial-models)
- [debt structuring (7)](https://www.intuitive-analytics.com/blog/topic/debt-structuring)
- [yield curve modeling (7)](https://www.intuitive-analytics.com/blog/topic/yield-curve-modeling)
- [decision support (6)](https://www.intuitive-analytics.com/blog/topic/decision-support)
- [financial analysis (6)](https://www.intuitive-analytics.com/blog/topic/financial-analysis)
- [financial model (6)](https://www.intuitive-analytics.com/blog/topic/financial-model)
- [libor (6)](https://www.intuitive-analytics.com/blog/topic/libor)
- [refunding efficiency (6)](https://www.intuitive-analytics.com/blog/topic/refunding-efficiency)
- [Finance Professionals (5)](https://www.intuitive-analytics.com/blog/topic/finance-professionals)
- [bond sizing (5)](https://www.intuitive-analytics.com/blog/topic/bond-sizing)
- [financial economy (5)](https://www.intuitive-analytics.com/blog/topic/financial-economy)
- [financial forecasting (5)](https://www.intuitive-analytics.com/blog/topic/financial-forecasting)
- [municipal swaps (5)](https://www.intuitive-analytics.com/blog/topic/municipal-swaps)
- [swaps (5)](https://www.intuitive-analytics.com/blog/topic/swaps)
- [tax-exempt financing (5)](https://www.intuitive-analytics.com/blog/topic/tax-exempt-financing)
- [Financial Software (4)](https://www.intuitive-analytics.com/blog/topic/financial-software)
- [Financial Technology (4)](https://www.intuitive-analytics.com/blog/topic/financial-technology)
- [Wall Street (4)](https://www.intuitive-analytics.com/blog/topic/wall-street)
- [callable bonds (4)](https://www.intuitive-analytics.com/blog/topic/callable-bonds)
- [refunding adjusted yield (4)](https://www.intuitive-analytics.com/blog/topic/refunding-adjusted-yield)
- [risk in finance (4)](https://www.intuitive-analytics.com/blog/topic/risk-in-finance)
- [tax risk (4)](https://www.intuitive-analytics.com/blog/topic/tax-risk)
- [Financial Engineers (3)](https://www.intuitive-analytics.com/blog/topic/financial-engineers)
- [Intuitive Analytics (3)](https://www.intuitive-analytics.com/blog/topic/intuitive-analytics)
- [Risk Management (3)](https://www.intuitive-analytics.com/blog/topic/risk-management)
- [SIFMA/LIBOR (3)](https://www.intuitive-analytics.com/blog/topic/sifmalibor)
- [SIFMA/LIBOR ratios (3)](https://www.intuitive-analytics.com/blog/topic/sifmalibor-ratios)
- [Spreadsheets (3)](https://www.intuitive-analytics.com/blog/topic/spreadsheets)
- [business process (3)](https://www.intuitive-analytics.com/blog/topic/business-process)
- [debt profiling (3)](https://www.intuitive-analytics.com/blog/topic/debt-profiling)
- [hedging (3)](https://www.intuitive-analytics.com/blog/topic/hedging)
- [monte carlo (3)](https://www.intuitive-analytics.com/blog/topic/monte-carlo)
- [press (3)](https://www.intuitive-analytics.com/blog/topic/press)
- [pv savings (3)](https://www.intuitive-analytics.com/blog/topic/pv-savings)
- [refundings (3)](https://www.intuitive-analytics.com/blog/topic/refundings)
- [variable rate (3)](https://www.intuitive-analytics.com/blog/topic/variable-rate)
- [BABs (2)](https://www.intuitive-analytics.com/blog/topic/babs)
- [Behavioral Finance (2)](https://www.intuitive-analytics.com/blog/topic/behavioral-finance)
- [CFaR (2)](https://www.intuitive-analytics.com/blog/topic/cfar)
- [Economist (2)](https://www.intuitive-analytics.com/blog/topic/economist)
- [Financial Services (2)](https://www.intuitive-analytics.com/blog/topic/financial-services)
- [Fischer Black (2)](https://www.intuitive-analytics.com/blog/topic/fischer-black)
- [Investment Banks (2)](https://www.intuitive-analytics.com/blog/topic/investment-banks)
- [Risk Metrics (2)](https://www.intuitive-analytics.com/blog/topic/risk-metrics)
- [Tax and Accounting Issues (2)](https://www.intuitive-analytics.com/blog/topic/tax-and-accounting-issues)
- [build america bonds (2)](https://www.intuitive-analytics.com/blog/topic/build-america-bonds)
- [cash flow at risk (2)](https://www.intuitive-analytics.com/blog/topic/cash-flow-at-risk)
- [database (2)](https://www.intuitive-analytics.com/blog/topic/database)
- [debt service chart (2)](https://www.intuitive-analytics.com/blog/topic/debt-service-chart)
- [financial risk (2)](https://www.intuitive-analytics.com/blog/topic/financial-risk)
- [linear algebra (2)](https://www.intuitive-analytics.com/blog/topic/linear-algebra)
- [muni (2)](https://www.intuitive-analytics.com/blog/topic/muni)
- [municipal default (2)](https://www.intuitive-analytics.com/blog/topic/municipal-default)
- [municipal investor (2)](https://www.intuitive-analytics.com/blog/topic/municipal-investor)
- [probability (2)](https://www.intuitive-analytics.com/blog/topic/probability)
- [public finance marketing (2)](https://www.intuitive-analytics.com/blog/topic/public-finance-marketing)
- [variable rate bonds (2)](https://www.intuitive-analytics.com/blog/topic/variable-rate-bonds)
- [(Un)Calculated Risk (1)](https://www.intuitive-analytics.com/blog/topic/uncalculated-risk)
- [Financial Management (1)](https://www.intuitive-analytics.com/blog/topic/financial-management)
- [Intellectual Property (1)](https://www.intuitive-analytics.com/blog/topic/intellectual-property)
- [Maximum Annual Debt Service (MADS) (1)](https://www.intuitive-analytics.com/blog/topic/maximum-annual-debt-service-mads)
- [Organization for Economic and Co-Operation and Dev (1)](https://www.intuitive-analytics.com/blog/topic/organization-for-economic-and-co-operation-and-dev)
- [Peter Orr (1)](https://www.intuitive-analytics.com/blog/topic/peter-orr)
- [SmartModels Stage III (1)](https://www.intuitive-analytics.com/blog/topic/smartmodels-stage-iii)
- [The Program for International Student Assessment ( (1)](https://www.intuitive-analytics.com/blog/topic/the-program-for-international-student-assessment)
- [Treasury Debt (1)](https://www.intuitive-analytics.com/blog/topic/treasury-debt)
- [VaR (1)](https://www.intuitive-analytics.com/blog/topic/var)
- [Weighted Average Life (1)](https://www.intuitive-analytics.com/blog/topic/weighted-average-life)
- [Win Smith (1)](https://www.intuitive-analytics.com/blog/topic/win-smith)
- [credit (1)](https://www.intuitive-analytics.com/blog/topic/credit)
- [cusip (1)](https://www.intuitive-analytics.com/blog/topic/cusip)
- [debt service graph (1)](https://www.intuitive-analytics.com/blog/topic/debt-service-graph)
- [escrow (1)](https://www.intuitive-analytics.com/blog/topic/escrow)
- [future tax rates (1)](https://www.intuitive-analytics.com/blog/topic/future-tax-rates)
- [interest rate markets (1)](https://www.intuitive-analytics.com/blog/topic/interest-rate-markets)
- [libor swaps (1)](https://www.intuitive-analytics.com/blog/topic/libor-swaps)
- [markets (1)](https://www.intuitive-analytics.com/blog/topic/markets)
- [monte carlo method (1)](https://www.intuitive-analytics.com/blog/topic/monte-carlo-method)
- [monte carlo model (1)](https://www.intuitive-analytics.com/blog/topic/monte-carlo-model)
- [municipal data (1)](https://www.intuitive-analytics.com/blog/topic/municipal-data)
- [negative arbitrage (1)](https://www.intuitive-analytics.com/blog/topic/negative-arbitrage)
- [optimization (1)](https://www.intuitive-analytics.com/blog/topic/optimization)
- [smartmodels utilities (1)](https://www.intuitive-analytics.com/blog/topic/smartmodels-utilities)
- [swaps that swallow town (1)](https://www.intuitive-analytics.com/blog/topic/swaps-that-swallow-town)
- [tax policy (1)](https://www.intuitive-analytics.com/blog/topic/tax-policy)
- [workflow (1)](https://www.intuitive-analytics.com/blog/topic/workflow)

[View all +](https://www.intuitive-analytics.com/blog/bid/13633/Are-munis-over-hedged-with-swaps-pt1#blog-sidebar-tags)