"If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is." - John von Neumann
I’ve landed on Earth from outer space, in these here United States (somehow feel right at home in Williamsburg…) and am trying to learn from you Earthlings how to calculate present value savings in public finance. During my journey here I tried to educate myself by reading a variety of materials including:
- Section 148 of Internal Revenue Code
- Minimize Negative Arbitrage or Maximize Savings?
- Refunding PV Savings - Arbitrage Yield or Zero Rates?
In the end, I’ve seen 2 methods. The first and more commonly used to date I'll call the Single Rate Method (SRM) which usually uses the arbitrage yield for discounting and the second I call the Zero Method (ZM) where different zero rates from the term curve are used to discount each cash flow. In order to understand these two methods better, I ran some refunding numbers and to my surprise what I discovered is that both methods are WRONG. I’m confused. Here’s what I did…
I took a hypothetical 20-year, 5% municipal bond callable at 102 in 3 years and ran some refundings, 20 to be exact. I used a single maturity, non-call par bond for each refunding from year 1 to year 20. Coupons/yields for the 20 individual refundings are shown in the 2nd column in the the table below.
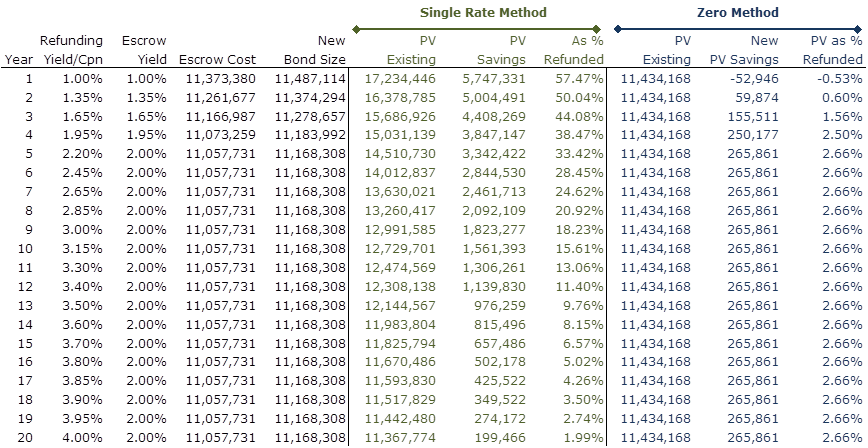
The maximum hypothetical escrow yield is 2% so the first 4 scenarios limit the escrow yield to the arbitrage yield of the respective refunding bond. To the size of the escrow (remember, 3 year call at 102) we add 1% for costs of issuance to arrive at the new bond size in the 'New Bond Size' column. In order to calculate PV savings we first take the present value of the existing bonds to maturity then subtract the present value of the new bond which is of course just the 'New Bond Size' under both methods.
Now in order to compare the two methods, we need to generate zero rates from the par curve which I discovered is not a common procedure in public finance circles. Nevertheless I do this easily using the handy Bootstrap function I found in these public finance utilities. Results and a proof of equality between discounting at 4% (the arb yield) and zero rates for the 20 year refunding bond scenario are shown in a table at the end of this post.
So how do these methods look? The first SRM method (green above) creates a massively different change in present value of the current debt, ignoring the valuation of the call feature itself for the moment. But the implication that the value of the existing bond to the borrower is as much as $17.2mm or as little as $11.4mm depending on the tenor of the refunding at best, lacks intuitive appeal. But it is exactly this calculated change in value of current debt that leads to the huge $5.7mm amount of PV savings for the 1% 1-year bond versus the paltry $199k savings in the 4%, 20 year bond scenario. This method must be wrong.
So let's look at the Zero Method (blue above). Using the zero rate discount factors (table below) the present value of existing debt is constant, which seems like an improvement. Even incorporating the call would be a constant offest against the noncall debt value for each scenario. But the present value of the new debt isn't changing either, except when the yield restriction kicks in. Therefore PV savings is identical in refunding scenarios from year 5 through year 20 but starts going DOWN as we refund with earlier maturities from year 4 and in. The larger present value of the new bond deal results from the arbitrage yield restriction on the ("100% efficient"!) escrow, hence decreasing savings. Therefore the Zero Method shows that refunding a 20-year 5% bond with a 1% 1-year bond actually creates negative savings. Though it may be in some sense more theoretically consistent, it's performance in aiding refunding criteria selection just doesn't seem spot on.
I'm new to your planet but we're trying to (re)finance a lot of infrastructure back home. What am I missing? Where have I gone astray? Can someone please help? Obi-Wan was busy...
You can download the Excel spreadsheet, 'PV Savings for Refundings-Methods Compared' used for this article here.
PROOF OF ZERO RATE EQUIVALENCE TO 4% PAR RATE, 20Yr BOND
| Zero Rate | 20Y | PV @ | |||
| t(30/360) | Par Rate | Zero Rate | DFs | New DS | Zero DFs |
| TOTALS = | 20,102,954 | 11,168,308 | |||
| 0.50 | 1.000% | 1.000% | 0.995025 | 223,366 | 222,255 |
| 1.00 | 1.000% | 1.000% | 0.990075 | 223,366 | 221,149 |
| 1.50 | 1.175% | 1.175% | 0.982586 | 223,366 | 219,477 |
| 2.00 | 1.350% | 1.353% | 0.973398 | 223,366 | 217,424 |
| 2.50 | 1.500% | 1.503% | 0.963248 | 223,366 | 215,157 |
| 3.00 | 1.650% | 1.657% | 0.951688 | 223,366 | 212,575 |
| 3.50 | 1.800% | 1.810% | 0.938874 | 223,366 | 209,713 |
| 4.00 | 1.950% | 1.966% | 0.924734 | 223,366 | 206,554 |
| 4.50 | 2.075% | 2.094% | 0.910507 | 223,366 | 203,376 |
| 5.00 | 2.200% | 2.226% | 0.895221 | 223,366 | 199,962 |
| 5.50 | 2.325% | 2.357% | 0.879102 | 223,366 | 196,362 |
| 6.00 | 2.450% | 2.491% | 0.861986 | 223,366 | 192,539 |
| 6.50 | 2.550% | 2.596% | 0.845621 | 223,366 | 188,883 |
| 7.00 | 2.650% | 2.705% | 0.828537 | 223,366 | 185,067 |
| 7.50 | 2.750% | 2.814% | 0.810954 | 223,366 | 181,140 |
| 8.00 | 2.850% | 2.924% | 0.792744 | 223,366 | 177,072 |
| 8.50 | 2.925% | 3.006% | 0.775988 | 223,366 | 173,329 |
| 9.00 | 3.000% | 3.090% | 0.758814 | 223,366 | 169,493 |
| 9.50 | 3.075% | 3.174% | 0.741436 | 223,366 | 165,612 |
| 10.00 | 3.150% | 3.260% | 0.723679 | 223,366 | 161,645 |
| 10.50 | 3.225% | 3.346% | 0.705775 | 223,366 | 157,646 |
| 11.00 | 3.300% | 3.435% | 0.687531 | 223,366 | 153,571 |
| 11.50 | 3.350% | 3.492% | 0.671574 | 223,366 | 150,007 |
| 12.00 | 3.400% | 3.551% | 0.655502 | 223,366 | 146,417 |
| 12.50 | 3.450% | 3.609% | 0.639448 | 223,366 | 142,831 |
| 13.00 | 3.500% | 3.670% | 0.623272 | 223,366 | 139,218 |
| 13.50 | 3.550% | 3.730% | 0.607159 | 223,366 | 135,619 |
| 14.00 | 3.600% | 3.793% | 0.590942 | 223,366 | 131,997 |
| 14.50 | 3.650% | 3.855% | 0.574819 | 223,366 | 128,395 |
| 15.00 | 3.700% | 3.920% | 0.558611 | 223,366 | 124,775 |
| 15.50 | 3.750% | 3.985% | 0.542508 | 223,366 | 121,178 |
| 16.00 | 3.800% | 4.051% | 0.526373 | 223,366 | 117,574 |
| 16.50 | 3.825% | 4.081% | 0.513463 | 223,366 | 114,690 |
| 17.00 | 3.850% | 4.112% | 0.500620 | 223,366 | 111,822 |
| 17.50 | 3.875% | 4.143% | 0.487951 | 223,366 | 108,992 |
| 18.00 | 3.900% | 4.175% | 0.475350 | 223,366 | 106,177 |
| 18.50 | 3.925% | 4.207% | 0.462930 | 223,366 | 103,403 |
| 19.00 | 3.950% | 4.240% | 0.450582 | 223,366 | 100,645 |
| 19.50 | 3.975% | 4.274% | 0.438411 | 223,366 | 97,926 |
| 20.00 | 4.000% | 4.308% | 0.426333 | 11,391,674 | 4,856,642 |
Calculated using Bootstrap in these Utilities.


Comments