"If we don't change direction soon, we'll end up where we're going" - Professor Irwin Corey
Since the dawn of refunding calculations, present value (PV) savings has been discounted using a single rate: usually the arbitrage yield or sometimes the all-in true interest cost (TIC) of the refunding bonds. However, core fixed income theory and today's computing power lead us toward a PV calculation that uses zero rates from the borrower’s funding curve to create discount factors instead of a single heroic rate.
But how much of a difference does this actually make to PV savings? Well of course that depends on a few things, specifically two “shapes.” The first is the shape of the yield curve and the second is the shape of the cash flow savings over time.
Tax-exempt yield curves have been reliably upward sloping in part due to the inherent tax preference uncertainty for investors. With upward sloping yield curves we’ll tend to have zero rates slightly higher than par rates of matching tenor. Below is a comparison of par rates and zero rates calculated using the Bootstrap function in SmartModels Utilities.
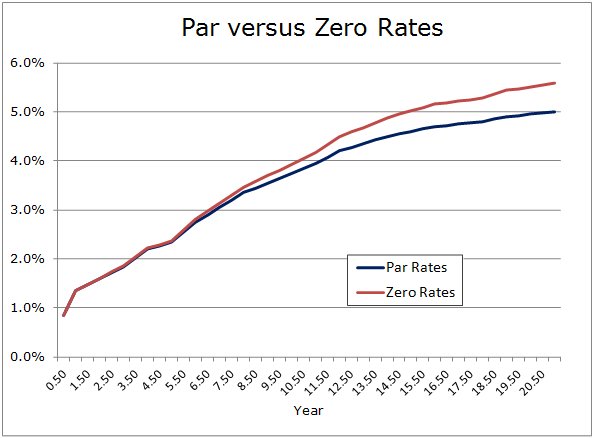
If in a refunding we create discount factors to each cash flow date from these zero rates instead of using a single rate such as the arbitrage yield, what happens to PV savings?
The answer is (drum roll…) "it depends". It depends on where the cash flow savings occurs in time. If the savings is roughly uniform across the deal structure then the over-discounting of the early cash flows when using a single blended rate will very closely offset the under-discounting of the later cash flows. A recent analysis we did showed the difference in dollar PV savings to be less than 0.1%.
However, if the savings is front-loaded (a popular structure with public entities these days) then discounting at rates from the zero curve will materially increase PV savings, anywhere from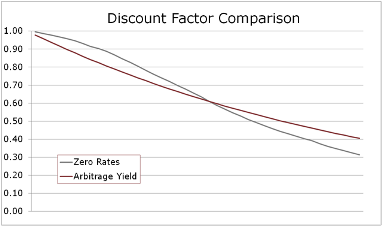 
3-10%. It’s the back-loaded savings deals that suffer when going to zero rates. Because we’re discounting at higher rates at the farthest points out on the curve, using zeros can decrease PV savings by 20% or more relative to using the good ol’ arbitrage yield. This can be seen easily when looking at a graph comparing discount factors (right).
So should we discount this way? In the past it would’ve been a pain in the derrier to do the bootstrapping to get zero rates from a par curve. But Bootstrap in SmartModels Utilities give you a trivial (and inexpensive!) way to get zeros rates to any cash flow date from an input par curve. It even handles all the messy interpolation for you. Today the question is “Why not?”
Comments