"Our lives improve only when we take chances - and the first and most difficult risk we can take is to be honest with ourselves."
Although it may not look related out of the gate, this post is a continuation of the prior post on LIBOR swaps over-hedging tax-exempt variable rate bonds. I want to start by looking at how one might build a reasonable interest rate model that would facilitate calculating this % LIBOR correctly, so that we expect to minimize the volatility of our synthetic fixed rate structure. Let's say your job is to build an interest rate model that captures the uncertainty inherent in SIFMA and LIBOR. This would be an unusual task for "quants" in public finance whose primary responsibility is coming up with accurate and often elaborate variations of present value ideas. The "model" used most frequently among front-line in investment bankers/advisors in this sector and in part due to an overreliance on spreadsheets looks something like this:
Some historic average over a selected time-period is used to create a static, flat, deterministic assumption for short rates over the time horizon of the analysis. This IS a type of interest rate model no doubt though one whose strength is not in capturing uncertainty/variability.
If an analyst were trying to create a SIFMA and LIBOR market model using two risk factors, perhaps un-intuitively s/he would not want to use "SIFMA" and "LIBOR" as the risk factors themselves. A detailed reason why is beyond the scope of this post (though you can find an outstanding thorough treatment here), but to put it simply, too much of the variability in SIFMA is also present in LIBOR. Let's face it, as US$ denominated short term interest rates, both SIFMA and LIBOR will be driven largely by changes in US monetary policy.
The better choice for a 2 factor model is LIBOR and SIFMA/LIBOR ratios. SIFMA/LIBOR ratios better reflect the unique component of risk in SIFMA itself i.e. the taxable/tax-exempt relationship. But how does this relate to the correlation impact on swap structure mentioned in the first post? It turns out that historically and on average, as LIBOR falls SIFMA/LIBOR ratios tend to go up and vice versa. In the industry vernacular bankers call this "yield compression" and it has a number of reasonable economic and technical explanations.

How do we capture this in a two-factor interest rate model that doesn't take a PhD to understand? For details on that you can read this and/or get a spreadsheet example. Suffice it to say, it really isn't so bad. To ultimately answer the original question, does this inverse relationship between rates (LIBOR) and ratios (SIFMA/LIBOR) impact the *right* percentage of LIBOR to use when hedging tax-exempt variable rate bonds? Absolutely. The graph below shows the LIBOR swap % that minimizes debt service volatility at different levels of expected correlation between LIBOR and SIFMA/LIBOR ratios.
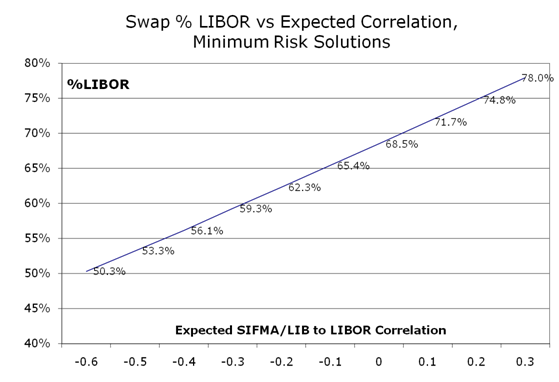
The bottom line is that using simple averages for this LIBOR swap hedge calculation does 2 things: a) ignores the fact that these structures are not equivalent to fixed rate bonds, a fact that's been sometimes painfully understood over the last 18 months and b) implicitly assumes a correlation of zero between rates and ratios which leads to a hedge ratio that is too high, and ultimately more LIBOR swap than is necessary. What are the cash flow and mark to market ramifications of this over-hedging? Stay tuned for the 3rd and final installment on this topic. In the meantime and if you're involved in the biz, how do YOU do this calculation?

Comments