---
title: Hull-White add Weight to New Interest Rate Modeling Research | Intuitive Analytics
description: New research by Hull and White confirms recent findings that interest rate changes indeed depend on their level, though in a different setting.
image: https://www.intuitive-analytics.com/hs-fs/file-642389577-png/images/hw_pic_small.png
---

# Hull-White add Weight to New Interest Rate Modeling Research

 Posted by Peter Orr on Apr 04, 2014

Last summer I wrote [an article](https://www.intuitive-analytics.com/blog/bid/60033/2013-Discovery-The-Missing-Link-in-Interest-Rate-Modeling) describing a missing link in rate modeling that had been discovered in exciting new research by Nick Deguillaume, [Ricardo Rebonato](http://en.wikipedia.org/wiki/Riccardo_Rebonato), and Andry Pogudin entitled [The nature of the dependence of the magnitude of rate moves on rates levels: a universal relationship](http://www.tandfonline.com/doi/abs/10.1080/14697688.2012.740569#.Uz6Rx_ldUb0). This mouthful offered two simple takeaways. First, accurately capturing *how *rates are expected to change, particularly over long time horizons, is central to every rate risk management decision we face. And second, that so-called “standard models” that don’t provide for the observed fact that rates tend to change differently depending on their level aren’t so realistic nor as a result, very good at informing interest rate decisions like refunding opportunities.

The other day Mr. Deguillaume emailed me to let me know their research apparently caught the attention of a couple other fellows who’ve been known to dabble in the dark arts of yield curve modeling, [John Hull](http://en.wikipedia.org/wiki/John_C._Hull) and [Alan White](http://en.wikipedia.org/wiki/Alan_White_(economist)).  This duo, a veritable LeBron James and Kevin Durant of financial economics, published a paper entitled [A Generalized Procedure for Building Trees for the Short Rate](http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2399615) just last month affirming the findings of Deguillame et al though in a completely different setting, no-arbitrage derivative pricing models. With the weight of this new research, what I’ve called this newly discovered missing link just got a heck of a lot bigger.

The Hull-White paper describes a more powerful, generalized Hull-White short-rate model that allows for interest rate changes to behave almost identically as described in the Deguillame et al research above i.e. rate changes are dependent on rate level. Specifically that rates below about 1.50% and above about 6% move in lognormal terms (as % of the rate level itself) and that rates in between this range move normally (in basis point terms). 

 ![HW Rate Graph](https://www.intuitive-analytics.com/hs-fs/file-642389577-png/images/hw_pic_small.png)

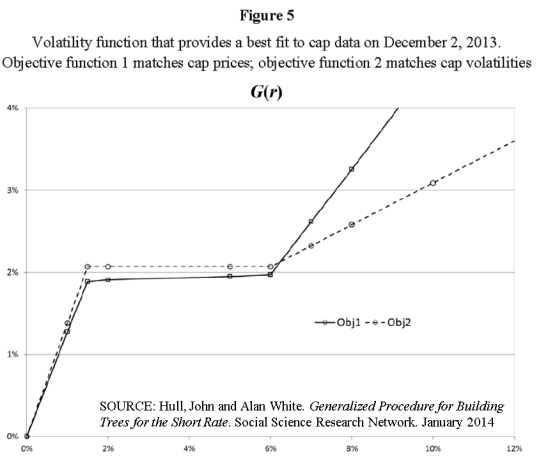
The fascinating result is that when they calibrate their modified model to market traded cap prices, the new “regime-shifting” rate volatility is **more than twice as good** at fitting all traded cap prices than standard normal (1st generation Hull-White) or lognormal (Black-Karasinski) interest rate models. 

Now their results, unlike Deguillame and company, were based on a grand total of a single day’s market data (2Dec13), hardly a robust data set. But I expect they or others pick up the torch very soon to test these results across more data.  

All of this points towards a sort of “Unified Theory” of interest rate modeling where a regime shifting feature is essential in every setting. Whether for the purpose of real-world option valuation for issuers or investors or no-arbitrage pricing models for interest rate derivatives dealers, a type of level dependent volatility is now *known to be* a best practice feature. Lest we get too inebriated by our own quantitative Kool-Aid, we must always keep in mind that everything here is a “model” and by definition only fractionally as complex as the real world. That said, it seems we’ve moved one step closer to realism when considering how to tackle the tough rate decisions that (public and private) corporations must face.

For more information on how to use these models in your organizations, give us a call (646.202.9446) or email info@intuitive-analytics.com.

### Comments

### Subscribe to our Articles

### Browse by Tag **

- [public finance (17)](https://www.intuitive-analytics.com/blog/topic/public-finance)
- [refunding (15)](https://www.intuitive-analytics.com/blog/topic/refunding)
- [public finance analytics (14)](https://www.intuitive-analytics.com/blog/topic/public-finance-analytics)
- [Financial Decisions (13)](https://www.intuitive-analytics.com/blog/topic/financial-decisions)
- [advance refunding (13)](https://www.intuitive-analytics.com/blog/topic/advance-refunding)
- [bond option (13)](https://www.intuitive-analytics.com/blog/topic/bond-option)
- [public finance software (12)](https://www.intuitive-analytics.com/blog/topic/public-finance-software)
- [call option (11)](https://www.intuitive-analytics.com/blog/topic/call-option)
- [interest rate model (9)](https://www.intuitive-analytics.com/blog/topic/interest-rate-model)
- [municipal finance software (9)](https://www.intuitive-analytics.com/blog/topic/municipal-finance-software)
- [SIFMA (8)](https://www.intuitive-analytics.com/blog/topic/sifma)
- [Financial Models (7)](https://www.intuitive-analytics.com/blog/topic/financial-models)
- [debt structuring (7)](https://www.intuitive-analytics.com/blog/topic/debt-structuring)
- [yield curve modeling (7)](https://www.intuitive-analytics.com/blog/topic/yield-curve-modeling)
- [decision support (6)](https://www.intuitive-analytics.com/blog/topic/decision-support)
- [financial analysis (6)](https://www.intuitive-analytics.com/blog/topic/financial-analysis)
- [financial model (6)](https://www.intuitive-analytics.com/blog/topic/financial-model)
- [libor (6)](https://www.intuitive-analytics.com/blog/topic/libor)
- [refunding efficiency (6)](https://www.intuitive-analytics.com/blog/topic/refunding-efficiency)
- [Finance Professionals (5)](https://www.intuitive-analytics.com/blog/topic/finance-professionals)
- [bond sizing (5)](https://www.intuitive-analytics.com/blog/topic/bond-sizing)
- [financial economy (5)](https://www.intuitive-analytics.com/blog/topic/financial-economy)
- [financial forecasting (5)](https://www.intuitive-analytics.com/blog/topic/financial-forecasting)
- [municipal swaps (5)](https://www.intuitive-analytics.com/blog/topic/municipal-swaps)
- [swaps (5)](https://www.intuitive-analytics.com/blog/topic/swaps)
- [tax-exempt financing (5)](https://www.intuitive-analytics.com/blog/topic/tax-exempt-financing)
- [Financial Software (4)](https://www.intuitive-analytics.com/blog/topic/financial-software)
- [Financial Technology (4)](https://www.intuitive-analytics.com/blog/topic/financial-technology)
- [Wall Street (4)](https://www.intuitive-analytics.com/blog/topic/wall-street)
- [callable bonds (4)](https://www.intuitive-analytics.com/blog/topic/callable-bonds)
- [refunding adjusted yield (4)](https://www.intuitive-analytics.com/blog/topic/refunding-adjusted-yield)
- [risk in finance (4)](https://www.intuitive-analytics.com/blog/topic/risk-in-finance)
- [tax risk (4)](https://www.intuitive-analytics.com/blog/topic/tax-risk)
- [Financial Engineers (3)](https://www.intuitive-analytics.com/blog/topic/financial-engineers)
- [Intuitive Analytics (3)](https://www.intuitive-analytics.com/blog/topic/intuitive-analytics)
- [Risk Management (3)](https://www.intuitive-analytics.com/blog/topic/risk-management)
- [SIFMA/LIBOR (3)](https://www.intuitive-analytics.com/blog/topic/sifmalibor)
- [SIFMA/LIBOR ratios (3)](https://www.intuitive-analytics.com/blog/topic/sifmalibor-ratios)
- [Spreadsheets (3)](https://www.intuitive-analytics.com/blog/topic/spreadsheets)
- [business process (3)](https://www.intuitive-analytics.com/blog/topic/business-process)
- [debt profiling (3)](https://www.intuitive-analytics.com/blog/topic/debt-profiling)
- [hedging (3)](https://www.intuitive-analytics.com/blog/topic/hedging)
- [monte carlo (3)](https://www.intuitive-analytics.com/blog/topic/monte-carlo)
- [press (3)](https://www.intuitive-analytics.com/blog/topic/press)
- [pv savings (3)](https://www.intuitive-analytics.com/blog/topic/pv-savings)
- [refundings (3)](https://www.intuitive-analytics.com/blog/topic/refundings)
- [variable rate (3)](https://www.intuitive-analytics.com/blog/topic/variable-rate)
- [BABs (2)](https://www.intuitive-analytics.com/blog/topic/babs)
- [Behavioral Finance (2)](https://www.intuitive-analytics.com/blog/topic/behavioral-finance)
- [CFaR (2)](https://www.intuitive-analytics.com/blog/topic/cfar)
- [Economist (2)](https://www.intuitive-analytics.com/blog/topic/economist)
- [Financial Services (2)](https://www.intuitive-analytics.com/blog/topic/financial-services)
- [Fischer Black (2)](https://www.intuitive-analytics.com/blog/topic/fischer-black)
- [Investment Banks (2)](https://www.intuitive-analytics.com/blog/topic/investment-banks)
- [Risk Metrics (2)](https://www.intuitive-analytics.com/blog/topic/risk-metrics)
- [Tax and Accounting Issues (2)](https://www.intuitive-analytics.com/blog/topic/tax-and-accounting-issues)
- [build america bonds (2)](https://www.intuitive-analytics.com/blog/topic/build-america-bonds)
- [cash flow at risk (2)](https://www.intuitive-analytics.com/blog/topic/cash-flow-at-risk)
- [database (2)](https://www.intuitive-analytics.com/blog/topic/database)
- [debt service chart (2)](https://www.intuitive-analytics.com/blog/topic/debt-service-chart)
- [financial risk (2)](https://www.intuitive-analytics.com/blog/topic/financial-risk)
- [linear algebra (2)](https://www.intuitive-analytics.com/blog/topic/linear-algebra)
- [muni (2)](https://www.intuitive-analytics.com/blog/topic/muni)
- [municipal default (2)](https://www.intuitive-analytics.com/blog/topic/municipal-default)
- [municipal investor (2)](https://www.intuitive-analytics.com/blog/topic/municipal-investor)
- [probability (2)](https://www.intuitive-analytics.com/blog/topic/probability)
- [public finance marketing (2)](https://www.intuitive-analytics.com/blog/topic/public-finance-marketing)
- [variable rate bonds (2)](https://www.intuitive-analytics.com/blog/topic/variable-rate-bonds)
- [(Un)Calculated Risk (1)](https://www.intuitive-analytics.com/blog/topic/uncalculated-risk)
- [Financial Management (1)](https://www.intuitive-analytics.com/blog/topic/financial-management)
- [Intellectual Property (1)](https://www.intuitive-analytics.com/blog/topic/intellectual-property)
- [Maximum Annual Debt Service (MADS) (1)](https://www.intuitive-analytics.com/blog/topic/maximum-annual-debt-service-mads)
- [Organization for Economic and Co-Operation and Dev (1)](https://www.intuitive-analytics.com/blog/topic/organization-for-economic-and-co-operation-and-dev)
- [Peter Orr (1)](https://www.intuitive-analytics.com/blog/topic/peter-orr)
- [SmartModels Stage III (1)](https://www.intuitive-analytics.com/blog/topic/smartmodels-stage-iii)
- [The Program for International Student Assessment ( (1)](https://www.intuitive-analytics.com/blog/topic/the-program-for-international-student-assessment)
- [Treasury Debt (1)](https://www.intuitive-analytics.com/blog/topic/treasury-debt)
- [VaR (1)](https://www.intuitive-analytics.com/blog/topic/var)
- [Weighted Average Life (1)](https://www.intuitive-analytics.com/blog/topic/weighted-average-life)
- [Win Smith (1)](https://www.intuitive-analytics.com/blog/topic/win-smith)
- [credit (1)](https://www.intuitive-analytics.com/blog/topic/credit)
- [cusip (1)](https://www.intuitive-analytics.com/blog/topic/cusip)
- [debt service graph (1)](https://www.intuitive-analytics.com/blog/topic/debt-service-graph)
- [escrow (1)](https://www.intuitive-analytics.com/blog/topic/escrow)
- [future tax rates (1)](https://www.intuitive-analytics.com/blog/topic/future-tax-rates)
- [interest rate markets (1)](https://www.intuitive-analytics.com/blog/topic/interest-rate-markets)
- [libor swaps (1)](https://www.intuitive-analytics.com/blog/topic/libor-swaps)
- [markets (1)](https://www.intuitive-analytics.com/blog/topic/markets)
- [monte carlo method (1)](https://www.intuitive-analytics.com/blog/topic/monte-carlo-method)
- [monte carlo model (1)](https://www.intuitive-analytics.com/blog/topic/monte-carlo-model)
- [municipal data (1)](https://www.intuitive-analytics.com/blog/topic/municipal-data)
- [negative arbitrage (1)](https://www.intuitive-analytics.com/blog/topic/negative-arbitrage)
- [optimization (1)](https://www.intuitive-analytics.com/blog/topic/optimization)
- [smartmodels utilities (1)](https://www.intuitive-analytics.com/blog/topic/smartmodels-utilities)
- [swaps that swallow town (1)](https://www.intuitive-analytics.com/blog/topic/swaps-that-swallow-town)
- [tax policy (1)](https://www.intuitive-analytics.com/blog/topic/tax-policy)
- [workflow (1)](https://www.intuitive-analytics.com/blog/topic/workflow)

[View all +](https://www.intuitive-analytics.com/blog/bid/74855/Hull-White-add-Weight-to-New-Interest-Rate-Modeling-Research#blog-sidebar-tags)